Teorema 5.7 - Clasificación de las superficies compactas

Enunciado

Si $S$ es una superficie compacta y conexa, entonces $S$ es homeomorfa a una de las siguientes superficies:

La esfera $S^{2}$ .
Una suma conexa de toros $T^{2} # \dots # T^{2}$ .
Una suma conexa de planos proyectivos ${RP}^{2} # \dots # {RP}^{2}$ .

Demostración

Objetivo

Aplicar transformaciones elementales a su presentación $P$ hasta llegar a uno de los siguientes casos:

P ≅ {\begin{cases} ⟨ a | a a^{- 1} ⟩, & presentación de S^{2}, \\ ⟨ a_{1}, b_{1}, \dots, a_{n}, b_{n} | a_{1} b_{1} a_{1}^{- 1} b_{1}^{- 1} \dots a_{n} b_{n} a_{n}^{- 1} b_{n}^{- 1} ⟩, & presentación de T^{2} # \dots # T^{2}, \\ ⟨ a_{1}, \dots, a_{n} | a_{1} a_{1} \dots a_{n} a_{n} ⟩, & presentación de {RP}^{2} # \dots # {RP}^{2} . \end{cases}

Para ello, separamos la demostración en 7 pasos, en cada uno de los cuales manipulamos $P$ para que cumpla una determinada condición^[1]. Tras el último paso, $P$ adoptará una de las formas anteriores. Durante la demostración, llamaremos aristas complementarias a aquellas que aparecen en $P$ como $a$ y $a^{- 1}$ , y aristas retorcidas a las que aparecen como $a$ y $a$ , o $a^{- 1}$ y $a^{- 1}$ .

Paso 1

Podemos suponer que $P$ tiene solo una palabra (o que el polígono tiene una sola cara).

Una consecuencia de que la superficie sea conexa es que si $P$ tuviera varias palabras, para cada una debería existir una letra que se identifique con otra arista de otra palabra distinta. Es decir, siempre que $P$ tenga varias palabras, para cada palabra $W_{i}$ de $P$ debe existir una arista $a \in W_{i}$ y otra palabra $W_{j}$ tal que o bien $a \in W_{j}$ o $a^{- 1} \in W_{j}$ . En caso contrario, en la realización geométrica, $W_{i}$ y las demás palabras serían disjuntas, formando así una separación que contradice la conexión de $S$ .

Ahora, si $P$ tiene más de una palabra, digamos $W_{1}$ y $W_{2}$ , por lo anterior existe una arista $a \in W_{1}$ que la conecta con $W_{2}$ , bien mediante $a$ o $a^{- 1}$ . De esta manera, se pueden pegar $W_{1}$ y $W_{2}$ ^[2] , obteniendo una presentación donde $W_{1}$ y $W_{2}$ se han sustituido por una única nueva palabra $W_{1}^{'} W_{2}^{'}$ .

Como el número de palabras de la presentación original es finito, mediante este proceso se obtiene una presentación equivalente compuesta por una sola palabra.

Paso 2

Podemos suponer que no hay pares de aristas complementarias adyacentes ( $W_{1} a a^{- 1} W_{2}$ ).

Si las hubiera, plegando por ellas desaparecen, excepto el caso en que solo tengamos ese par de letras ( $W_{1}, W_{2} = \emptyset$ ); no obstante, entonces la superficie sería una esfera, que se trata de una de las formas canónicas que buscábamos obtener.

Paso 3

Podemos suponer que todos los pares de aristas retorcidas son adyacentes.

Supongamos que tenemos $⟨ V a W a ⟩$ , con $V, W \neq \emptyset$ . Primero, cortamos por el medio:

⟨ V a b, b^{- 1} W a ⟩

luego, rotamos y reflejamos la segunda palabra:

⟨ b V a, a^{- 1} W^{- 1} b ⟩;

por último, pegamos por $a$ y rotamos de nuevo, llegando a $⟨ b b V W^{- 1} ⟩$ , donde las aristas retorcidas ya son adyacentes. Este proceso se puede repetir un número finito de veces hasta conseguir que todo par de aristas retorcidas sean adyacentes.

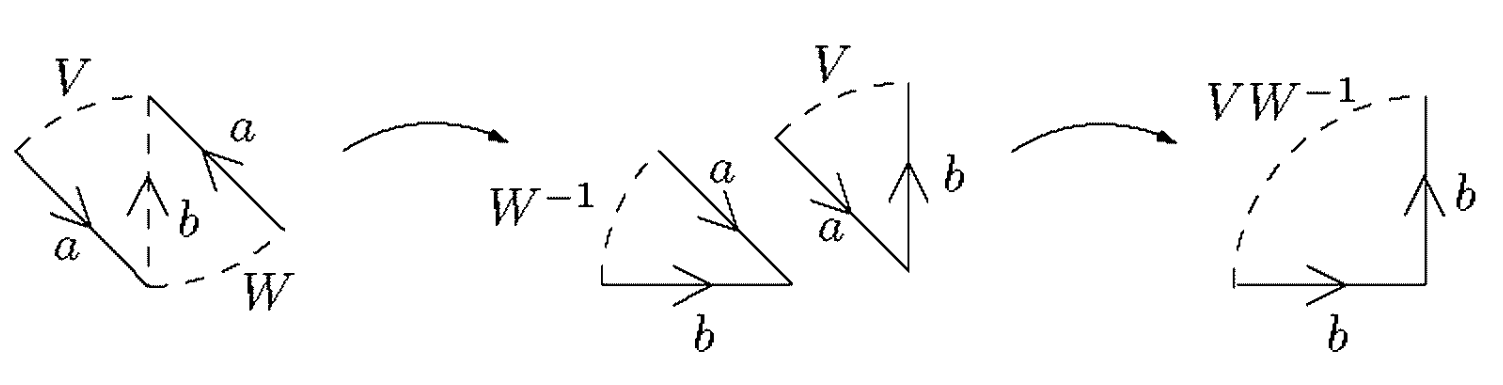
$paso3.png$

Paso 4

Podemos suponer que el polígono tiene todos sus vértices identificados. ^[3]

Sea $p : P \to S$ la proyección al cociente, esto es, $p (v) = [v]$ . Si no todos los vértices están identificados, entonces existen vértices $v, w \in P$ y una arista $a (v \to w)$ con $p (v) \neq p (w)$ .
Ahora, la arista $b$ que termina en $v$ no puede ser ni $a$ , ya que entonces $p (v) = p (w)$ , ni tampoco $a^{- 1}$ , pues se tendría la secuencia $a^{- 1} a$ y, al aplicar de nuevo el paso 2, llegaríamos también a la igualdad.
Por tanto, concluimos que la arista b es distinta, y parte del vértice $x$ . Es decir, tenemos $b (x \to v)$ .

Por la definición de presentación poligonal, la letra $b$ debe aparecer en otro sitio de la presentación.
Suponemos que aparece $b^{- 1}$ (si fuese $b$ sería análogo salvo una reflexión). Tenemos entonces una secuencia $⟨ b a X b^{- 1} Y ⟩$ , con $X$ e $Y$ cadenas arbitrarias de la presentación. Podemos suponer que $X, Y \neq \emptyset$ porque:

Si $X$ fuese vacío, por la definición de $b$ , el vértice al que llega $b^{- 1}$ en nuestra cadena sería $w$ ^[4]. Pero entonces $p (v) = p (w)$ ^[5], lo que contradice la hipótesis.
Si $Y$ fuese vacío, rotando obtendríamos dos aristas adyacentes $b$ y $b^{- 1}$ y estaríamos en el paso 2.

Ahora, cortando por una nueva arista $c (w \to x)$ y rotando para pegar por $b$ (si se tuviera otra $b$ , se podría reflejar) obtenemos:

⟨ b a X b^{- 1} Y ⟩ ≅ ⟨ b a c, c^{- 1} X b^{- 1} Y ⟩ ≅ ⟨ a c b, b^{- 1} Y c^{- 1} X ⟩ ≅ ⟨ a c Y c^{- 1} X ⟩

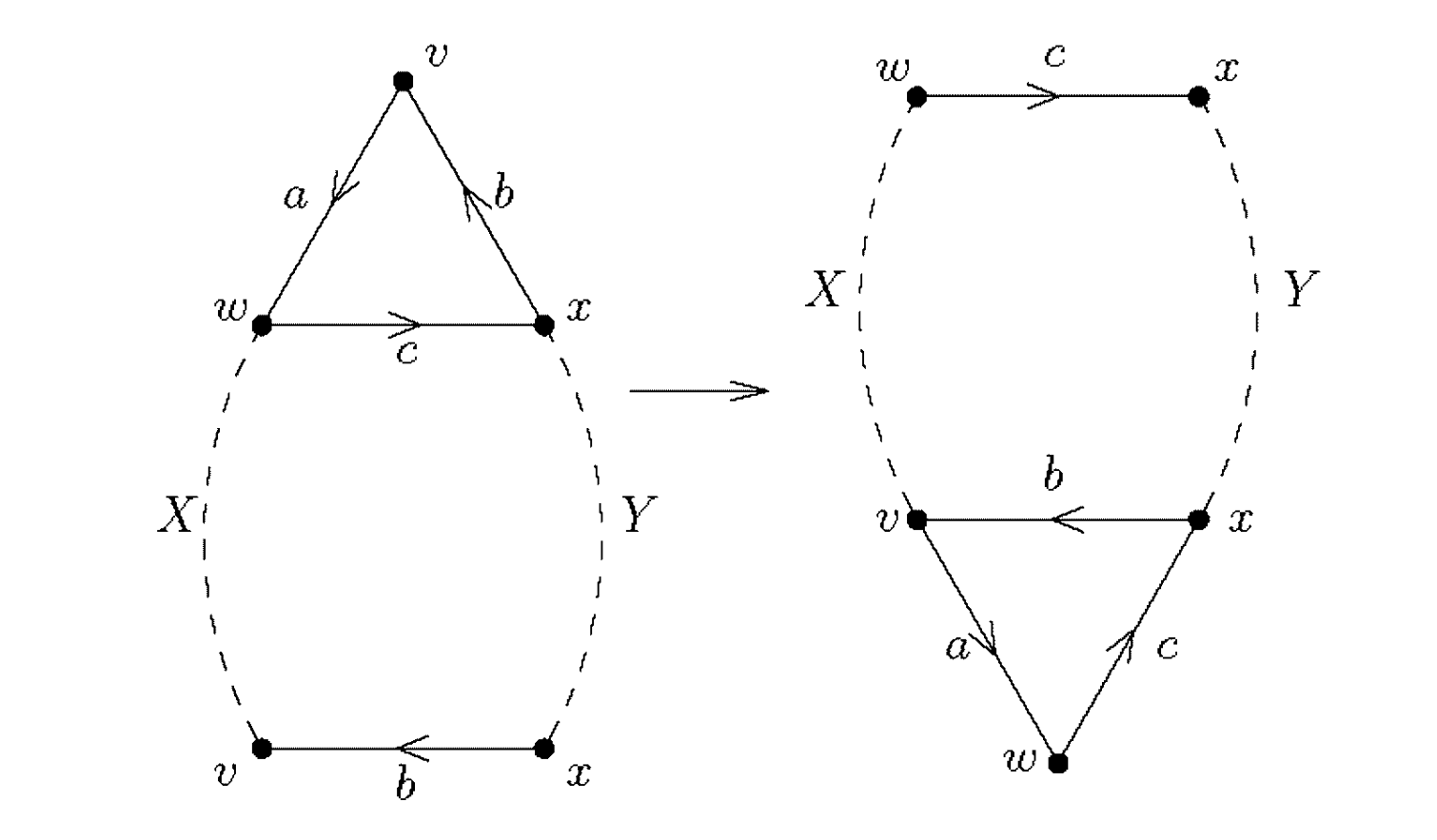
$paso4.png$

Esta es una presentación equivalente donde hemos reducido la cantidad de vértices que se identifican con $v$ en una unidad ^[6]. Una cantidad finita de iteraciones de este proceso elimina la clase de equivalencia de vértices $v$ . Luego, repitiendo para cada clase de equivalencia de vértices, llegamos a que solo puede quedar una.

Paso 5

Si aparece un par $a, a^{- 1}$ , entonces hay otro par $b, b^{- 1}$ intercalado, es decir, de la forma $a \dots b \dots a^{- 1} \dots b^{- 1}$ .

Si no fuese así, tendríamos una presentación de la forma $a X a^{- 1} Y$ , donde $X$ e $Y$ no comparten aristas. Además, tampoco podrían tener en común una letra $b$ por el paso 3. Esto significa, al mismo tiempo, que $X$ e $Y$ no comparten vértices, porque si lo hicieran, alguna de las aristas que salen de estos, al identificarse en la proyección al cociente, tendría que estar en ambos.

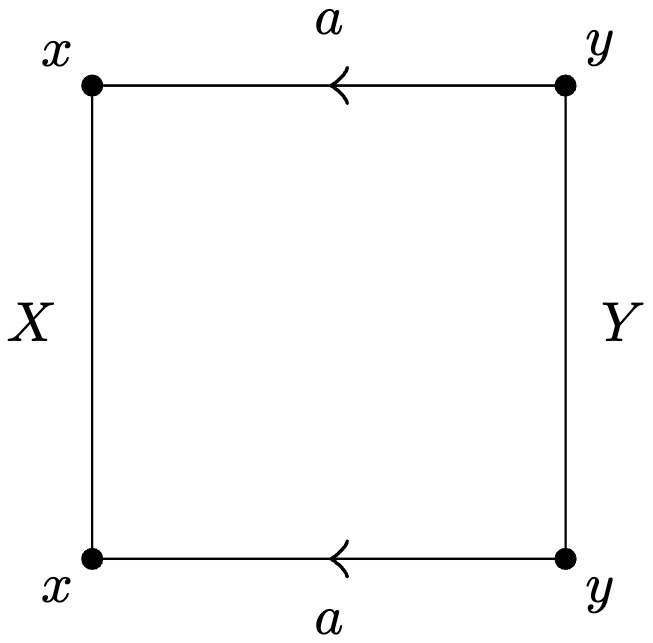
$paso5.png|300$

En particular, los vértices finales de $a$ y $a^{- 1}$ , que están ambos en $X$ , solo pueden identificarse con vértices de $X$ . Por otro lado, los vértices iniciales de $a$ y $a^{- 1}$ , que están ambos en $Y$ , solo pueden identificarse con vértices de $Y$ . Por tanto, existen dos clases de equivalencia de vértices distintas, lo que contradice el paso 4. Por esto motivo, los pares de aristas complementarias deben estar intercalados.

Paso 6

Podemos suponer que los pares de aristas del paso 5 aparecen consecutivos.

Tenemos ahora una cadena $⟨ a X b Y a^{- 1} Z b^{- 1} W ⟩$ . Empezamos rotando la presentación original, para cortar desde el final de $X$ al inicio de $W$ :

⟨ a X b Y a^{- 1} Z b^{- 1} W ⟩ ≅ ⟨ W a X b Y a^{- 1} Z b^{- 1} ⟩ ≅ ⟨ W a X c, c^{- 1} b Y a^{- 1} Z b^{- 1} ⟩

A continuación, se pega por $a$ , para lo cual tenemos primero que rotar:

⟨ W a X c, c^{- 1} b Y a^{- 1} Z b^{- 1} ⟩ ≅ ⟨ X c W a, a^{- 1} Z b^{- 1} c^{- 1} b Y ⟩ ≅ ⟨ X c W Z b^{- 1} c^{- 1} b Y ⟩

Posteriormente, cortamos desde el principio de $b^{- 1}$ hasta el final de $c$ :

⟨ X c W Z b^{- 1} c^{- 1} b Y ⟩ ≅ ⟨ c^{- 1} b Y X c W Z b^{- 1} ⟩ ≅ ⟨ c^{- 1} b Y X c d, d^{- 1} W Z b^{- 1} ⟩

Por último, rotando y pegando por $b$ conseguimos que las cuatro aristas queden consecutivas:

⟨ c^{- 1} b Y X c d, d^{- 1} W Z b^{- 1} ⟩ ≅ ⟨ Y X c d c^{- 1} b, b^{- 1} d^{- 1} W Z ⟩ ≅ ⟨ Y X c d c^{- 1} d^{- 1} W Z ⟩

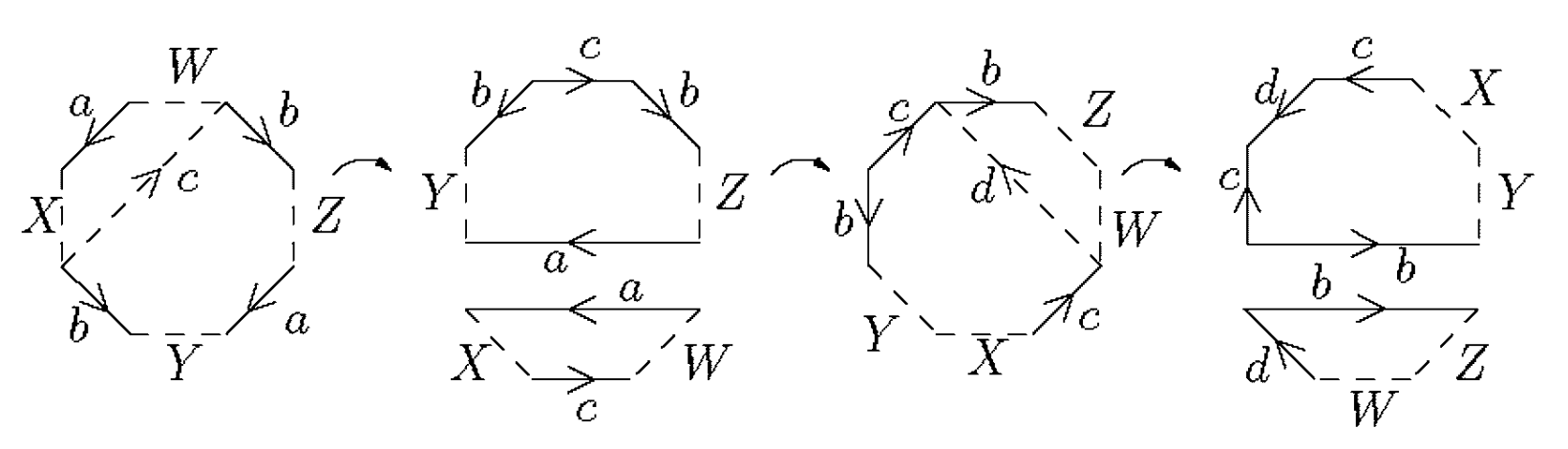
$paso6.png$

Ahora tan solo habría que repetir esto para todos los pares de aristas intercalados no consecutivos.

Paso 7

La superficie $S$ es homeomorfa a $T^{2} # \dots # T^{2}$ , o bien a ${RP}^{2} # \dots # {RP}^{2}$ .

En este punto, la presentación solo puede contener los siguientes tipos de elementos:

Parejas de aristas complementarias consecutivas, de la forma $a b a^{- 1} b^{- 1}$ .
Aristas retorcidas de la forma $a a$ .

De esta manera, teniendo en cuenta que la presentación poligonal de un toro viene dada precisamente por la primera forma, mientras que la de un plano proyectivo por la segunda, si solo hubiese aristas de una de estas dos formas la superficie sería homeomorfa a una suma conexa de toros o de planos proyectivos, respectivamente.

Nos queda ver qué ocurre en el caso de que $P$ contenga ambos grupos de aristas. Supongamos que existen un grupo de aristas complementarias $a b a^{- 1} b^{- 1}$ y otro de aristas retorcidas $c c$ . Entonces, teniendo en cuenta el lema 5.6, se podría transformar cada par toro-proyectivo, eliminando todos los toros y acabando con un número finito de planos proyectivos.

Concluyendo:

Si $P$ tiene un solo par de aristas complementarias adyacentes, es homeomorfa a una esfera.
Si $P$ tiene solo aristas complementarias alternadas, es homeomorfa a una suma conexa de toros.
Si $P$ tiene solo aristas retorcidas, es homeomorfa a una suma conexa de planos proyectivos.
Si $P$ tiene ambos tipos de aristas, es homeomorfa a una suma conexa de planos proyectivos.

Se hará un abuso de notación al llamar $P$ tanto a la presentación original como a la presentación $P^{'}$ obtenida tras aplicar una transformación elemental. ↩︎
Aplicando rotaciones y reflejos de ser necesario. ↩︎
Esto es, solo hay un vértice al pasar al cociente. ↩︎
Ya que la arista es $a (v \to w)$ y serían adyacentes. ↩︎
Donde termina $a$ es $w$ , que coincidiría con donde acaba $b$ , esto es, $w = v$ . ↩︎
Claramente no puede reducirse la cantidad de vértices total de la figura, pero sí el número de aquellos que se identifican con $v$ ↩︎